Численное исследование пространственно-временной структуры и свойств φ 4-осциллонов в шаре конечного радиуса
Е.В. Земляная1, А.А. Боголюбская1, М.В. Башашин1,
Н.В. Алексеева2, И.В. Барашенков1,2
1 Лаборатория информационных технологий ОИЯИ
2 Кейптаунский университет, факультет математики, Южная Африка
Рассматривается уравнение теории φ4, имеющее ряд приложений в физике и математике:
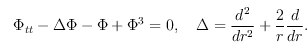
Исследуются слабоизлучающие сферически-симметричные осциллоны этого уравнения – долгоживущие пульсирующие состояния, характеризующиеся близкими к константам значениями амплитуды и частоты пульсаций. Такие состояния в модели φ 4 можно аппроксимировать стоячими волнами в шаре конечного радиуса. При этом периодические по времени стоячие волны определяются как решения краевой задачи на цилиндрической поверхности.
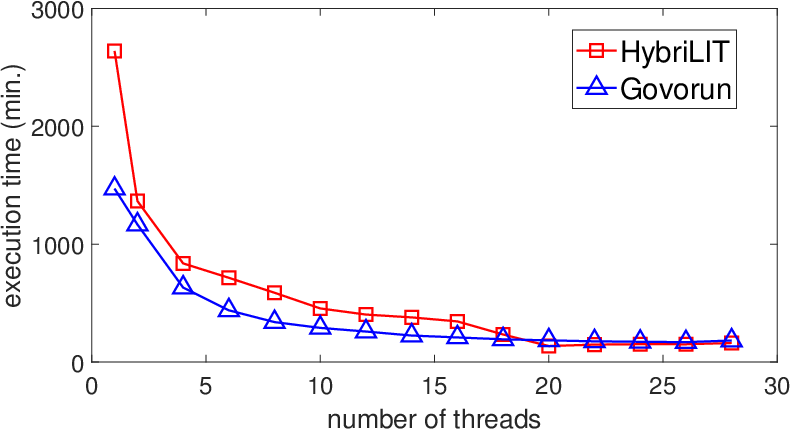
Численное исследование сводится к численному продолжению локализованных решений вышеуказанной двумерной граничной задачи с использованием ньютоновских итераций для ее решения при каждом фиксированном значении параметра частоты. Устойчивость полученных таким образом волн к малым сферически симметричным возмущениям классифицируется на основе вычисления соответствующих множителей Флоке, что требует значительных затрат компьютерного времени. Для ускорения вычислений реализована параллельная версия MATLAB-программы, обеспечившая уменьшение времени счета от 10 до 20 раз на ресурсах учебно-тестового полигона HybriLIT и суперкомпьютера «Говорун» (см. рис. 1).
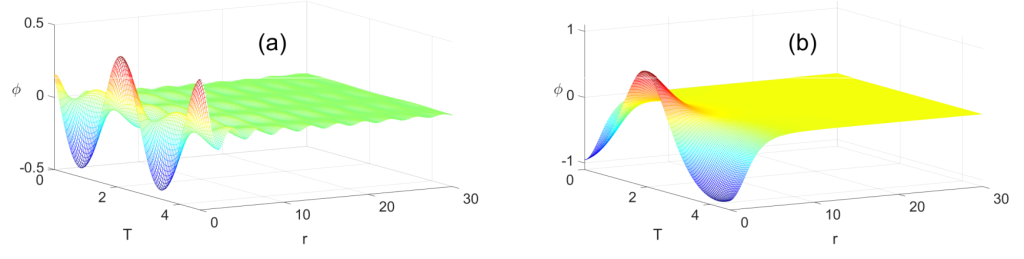
В результате проведенного исследования найдены два сосуществующих класса стоячих волн (рис. 2). Показано, что зависимость энергии волн от частоты осцилляций характеризуется наличием резонансных пиков, где ветви двух типов волн объединяются в результате бифуркаций удвоения периода. Найдены интервалы частот, где волны оказываются устойчивыми.
Продолжающиеся в настоящее время исследования направлены на повышение точности вычислительной схемы и на детальное исследование интервалов устойчивости в зависимости от значения радиуса.
Публикации:
N.V. Alexeeva, I.V. Barashenkov, A.A. Bogolubskaya, E.V. Zemlyanaya. Understanding oscillons: Standing waves in a ball // Phys. Rev. D V. 107, 2023, 076023
E. V. Zemlyanayaa, A. A. Bogolubskayaa, M. V. Bashashin, N. V. Alexeeva. The φ4 Oscillons in a Ball: Numerical Approach and Parallel Implementation // Physics of Particles and Nuclei, Vol. 55, No. 3, 2024, 505-508.

