Отчет
об использовании вычислительных ресурсов гетерогенной платформы HybriLIТ
Иван Георгиев Христов, Радослава Данаилова Христова,
Факультет Математики и Информатики, Софийский Университет, Болгария
e-mails: christov_ivan@abv.bg , radoslava@fmi.uni-sofia.bg
1. Название решаемой задачи (на русском и английском языках).
Численное исследование комбинированных явных-неявных методов Тейлора с разных порядков точности для решений Гамильтоновых систем.
2. Список научного коллектива
С.Н. Димова, И.Г. Христов, Р.Д. Христова, И.В. Пузынин, Т.П. Пузынина, З.А. Шарипов, Н.Г. Шегунов, З.К. Тухлиев.
3. Краткое описание решаемой задачи с указанием темы ПТП ОИЯИ, в рамках которой решалась задача
Проведено сравнение между классическим методом Верле и комбинированными (гибридными) методами Тейлора различного порядка точности для решения некоторых гамильтоновых систем. Цель исследования — подтвердить наши ожидания, что эти методы ведут себя как симплектические с точки зрения сохранения энергии, и что в случаях, где требуется высокая точность, они могут превосходить стандартный метод Verlet второго порядка. Также реализована параллельная программа с использованием технологии OpenMP для вычисления много независимых траектории. Используя ресурсы одного CPU узла Учебно-тестового полигона HybriLIТ было достигнуто ускорение в 37 раз.
Работа выполнена в рамках тематического плана ОИЯИ, 05-6-1119-2014/2019 «Методы, алгоритмы и программное обеспечение для моделирования физических систем, математической обработки и анализа экспериментальных данных»
4. Описание полученных за отчетный период результатов.
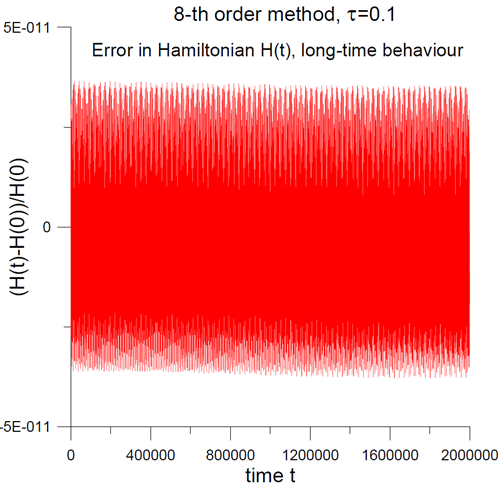
- Все численные результаты подтверждают наши ожидания, что гибридные методы Тейлора отлично сохраняет энергию (смотри Фигура 1).
- Среднее число итераций для решения неявного этапа зависит от размер шага. Среднее число итераций стремится к единице, когда шаг стремится к нулю. Это означает, что работа для одного шага гибридного метода сравнима с работой аналогичного явного метода Тейлора (смотри Таблица 1).
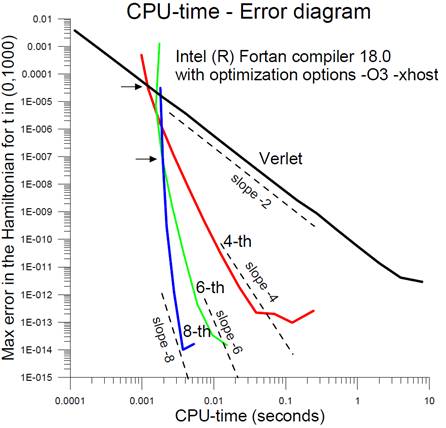
- В случаях, где требуется высокая точность, наши методы превосходят стандартный метод Verlet второго порядка (смотри Фигура 2).
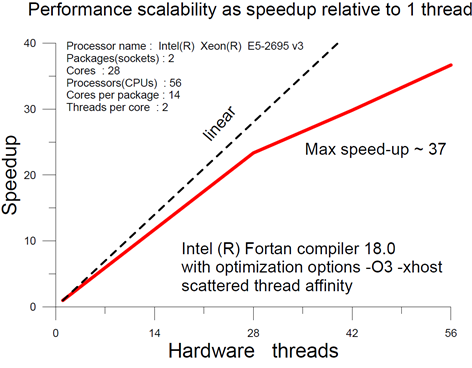
- Для вычисления большого количества (например 1000) независимых траектории нашим методом, мы достигли ускорения в 37 раз используя ресурсы одного CPU узла учебно-тестового полигона HybriLIТ (смотри Фигура 3).

5. Описание использования вычислительных ресурсов, указать фактически использованное количество CPU ядер, количество графических ускорителей (или CUDA ядер), использованный объем дискового хранилища. Привести перечень ПО, использованный для решения задачи.
Мы использовали ресурсы одного CPU узла Учебно-тестового полигона HybriLIT (28 ядер, 56 нитей). Небольшой объем использованного дискового хранилища.
6. Перечень опубликованных работ, в которых выражена благодарность HybriLIT за использование ресурсов.
Подтверждаем, что результаты, представленные в отчете могут быть опубликованы на сайте HybriLIT.
- N. Dimova, I. G. Hristov, R. D. Hristova, I. V. Puzynin, T. P. Puzynina, Z. A. Sharipov, N. G. Shegunov, Z. K. Tukhliev, Combined explicit-implicit taylor series methods CEUR Workshop Proceedings, GRID 2018 International Conference «Distributed Computing and Grid-technologies in Science and Education» 2018, volume 2267, 2018, pp.544-548, ISSN (online):1613-0073

