Еремин Роман Александрович, c.н.с. Международного научно-исследовательского центра по теоретическому материаловедению, Самарский университет и Самарский государственный технический университет (Пользователь: ererom)
Историческая справка
В 2016-2017 гг. сотрудниками Международного научно-исследовательского центра по теоретическому материаловедению (МНИЦТМ) совместно с сотрудниками Лаборатории нейтронной физики им. И.М. Франка нами была выполнена работа по квантовомеханическому моделированию разупорядоченной структуры коммерческого катодного материала NCA, изученного ранее методами нейтронной дифракции в процессе заряда-разряда электрохимического источника тока на его основе. В результате проведенного исследования была опубликована серия научных работ [1–3] (Journal of Physical Chemistry C – IF 4.5). Оригинальность указанных работ состояла в (1) генерации и квантовомеханическом моделировании полных композиционно-конфигурационных пространств (ККП) изученных соединений, т.е. всех возможных неэквивалентных реализаций структуры (более 20 000 структур для NCA) с учетом разупорядочения вследствие легирования и деинтеркаляции рабочего иона, (2) топологическом анализе построенных КПП с привлечением методов машинного обучения и (3) качественном описании экспериментальных данных в рамках модельных подходов.
В названных работах для составления ККП применялся геометрико-топологический анализ, реализованный в комплексе ToposPRO [4] на базе МНИЦТМ, а существующие программные реализации выбора неэквивалентных структурных реализаций на основе анализе симметрии исходной кристаллической структуры вещества, такие как SOD [5] и SuperCell [6], применялись как средства контроля получаемых результатов. Кроме того, как было позже обнаружено, названные программные решения обладают рядом принципиальных и ситуативных ограничений. Так, программа SOD не реализует возможность разупорядочения различных кристаллографических позиций или комбинации различных типов дефектов в одной позиции, а SuperCell имеет ограничения запуска по сложности КПП даже в тех случаях, когда в рамках модели предусматривается использование редуцированных (например, на основе случайного выбора структур) КПП. В начале 2018 была завершена работа по написанию прототипа Mathematica-программы для моделирования ККП, использующей последовательную схему включения различных типов дефектов, ранее реализованную в работах [1–3] вручную, а также возможность выбора редуцированных КПП.
Направления текущих работы с привлечением гетерогенной платформе HybriLIT:
1. Сэмплирование КПП легированных твердотельных электролитов
Работы по моделированию свойств проводимости легированных твердотельных электролитов были начаты сотрудниками МНИЦТМ в 2015 году, в результате на основании случайного выбора реализаций структуры легированного твердотельного электролита K(Fe,Ti)O2, была выполнена научная работа [7]. В рамках текущих работ мы расширяем методику на основе генерации полных ККП, ранее использованную при моделировании катодного материала, на случай твердотельного электролита K(Fe,Ti)O2 с минимальными уровнями легирования.Для генерации конфигурационных пространств, содержащих наборы возможных реализаций пяти неэквивалентных элементарных переходов токопроводящего иона в кристалле K(Fe,Ti)O2, была выполнена следующая процедура. В качестве атомов, маркирующих начало и конец перехода, были заданы 2 атома AMg, соответствующих атомному сорту магния, внедряемые в подрешетку мигрирующего иона. При этом, в случае рассмотрения процесса токопереноса как совокупности ион-вакансия обменов, одной вакансии в модельной ячейке соответствует 2 атома AMg. Полные конфигурационные пространства формировались для изученных уровней легирования c использованием ПО SuperCell, после чего из полученных конфигурационных пространств выбираются множества «корректных» переходов, т.е. таких модельных ячеек, расстояния между позициями атомов AMg в которых не превосходило порогового значения 4 Å (согласно данным из [7]). Примеры модельных ячеек, задающих переходы токопроводящего иона, приводятся на рисунке 1.
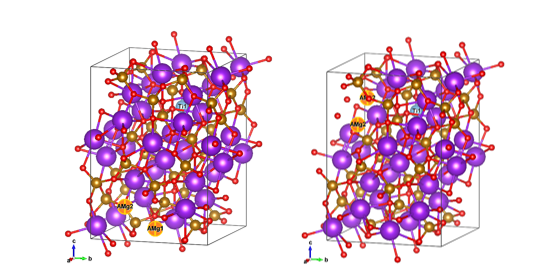
После генерации соответствующих ККП, будет выполнено квантовохимическое моделирование процессов ионного транспорта. По результатам проводимого исследования в 2019 году запланирована публикация статьи (предположительно, журнал Chemical Physics – IF 2.5)
2. Сэмплирование КПП интерметаллических Sc-Pt, Sc-Pd соединений (работы выполняются совместно с Университетом г. Генуи, Италия, Миланским университетом, Италий, Фрайбергской горной академией, Германия)
Версия Mathematica-программы была использована для генерации и обработки редуцированных ККП для Sc-Pt и Sc-Pd интерметаллидов. Синтез последнего из названных объектов исследования был выполнен сотрудниками МНИЦТМ в 2016 году, после чего экспериментальное исследование методами рентгеновского анализа показало, что структура характеризуется разупорядочением некоторых кристаллографических позиций. В результате генерации редуцированных ККП для Sc-Pd интерметаллида были выбраны 1041 неэквивалентная конфигурация (с применением SuperCell), и выполнено их квантовомеханическое моделирование. Для проведения геометрико-топологического анализа построенное ККП было модифицировано с использованием Mathematica-программы (добавлены центройды атомных группировок, проведено введение эффективных атомов, соответствующих вакансиям).В случае Sc-Pt систем, для которых непосредственное использование ПО SuperCell не представлялось возможным ввиду высокой сложности итоговых КПП, с использованием Mathematica-программы построен минимально возможный срез КПП (1 случайная конфигурация для каждой из 675 структурных моделей), который впоследствии будет расширен с учетом результатов квантовомеханического моделирования.
По результатам проводимого исследования в 2019 году запланирована публикация статьи (предположительно, журнал Journal of the American Chemical Society – IF 14.3)
Литературные источники
- R.A. Eremin, P.N. Zolotarev, O.Y. Ivanshina, I.A. Bobrikov, Li(Ni,Co,Al)O2 Cathode Delithiation: A Combination of Topological Analysis, Density Functional Theory, Neutron Diffraction, and Machine Learning Techniques, J. Phys. Chem. C. 121 (2017) 28293−28305. doi:10.1021/acs.jpcc.7b09760.
- R. Eremin, P. Zolotarev, I. Bobrikov, Delithiated states of layered cathode materials : doping and dispersion interaction effects on the structure, EPJ Web Conf. 177 (2018) 02001.
- P. Zolotarev, R. Eremin, Topology-based description of the NCA cathode configurational space and an approach of its effective reduction, EPJ Web Conf. 177 (2018) 02005.
- V.A. Blatov, A.P. Shevchenko, D.M. Proserpio, Applied Topological Analysis of Crystal Structures with the Program Package ToposPro, Cryst. Growth Des. 14 (2014) 3576–3586. doi:10.1021/cg500498k.
- R. Grau-Crespo, S. Hamad, C.R.A. Catlow, N.H. de Leeuw, Symmetry-adapted configurational modelling of fractional site occupancy in solids, J. Phys. Condens. Matter. 19 (2007) 256201. doi:10.1088/0953-8984/19/25/256201.
- K. Okhotnikov, T. Charpentier, S. Cadars, Supercell program: a combinatorial structure-generation approach for the local-level modeling of atomic substitutions and partial occupancies in crystals, J. Cheminform. 8 (2016) 17. doi:10.1186/s13321-016-0129-3.
- N.V. Proskurnina, V.I. Voronin, G.S. Shekhtman, L.N. Maskaeva, N.A. Kabanova, A.A. Kabanov, V.A. Blatov, Ionic Conductivity in Ti-Doped KFeO2: Experiment and Mathematical Modeling, J. Phys. Chem. C. 121 (2017) 21128–21135. doi:10.1021/acs.jpcc.7b05164.
- K. Momma, F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr. 44 (2011) 1272–1276. doi:10.1107/S0021889811038970.

