Параллельные алгоритмы для исследования системы длинных джозефсоновских переходов

Параллельные алгоритмы для исследования системы длинных джозефсоновских переходов*

М.В. Башашин^1,3, Е.В. Земляная^1,3, М.И. Зуев¹, А.В. Нечаевский¹, И. Р. Рахмонов², Д.В. Подгайный¹, О.И. Стрельцова^1,3, Ю.М. Шукринов^2,3
¹Лаборатория информационных технологий ОИЯИ
²Лаборатория теоретической физики им. Н.Н. Боголюбова ОИЯИ
³Государственный университет «Дубна»

*Исследование выполнено за счет гранта Российского научного фонда (проект № 18-71-10095).

В работе представлены результаты исследования эффективности параллельных реализаций вычислительной схемы для расчета вольт-амперных характеристик системы длинных джозефсоновских переходов [1,2]. В работах [3,4] дано описание разработанного параллельного алгоритма и представлены результаты тестирования MPI-версии расчета ВАХ в зависимости от вычислительных параметров. В настоящей работе представлены разработанные параллельные реализации на основе другого инструментария: OpenMP-реализация для проведения расчетов на системах с общей памятью, CUDA-реализация для проведения расчетов на графических процессорах NVIDIA. Разработка, отладка и профилирование параллельных приложений проводились на учебно-тестовом полигоне гетерогенной вычислительной платформы HybriLIT, а расчеты проводились на суперкомпьютере ГОВОРУН [2].

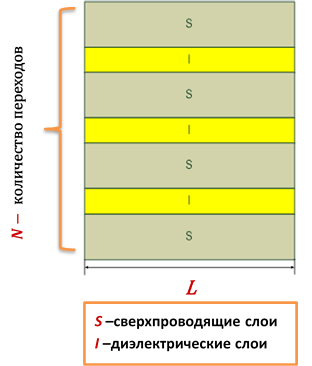Постановка задачи. Рассматривается обобщенная модель, учитывающая индуктивную и емкостную связь между длинными джозефсоновскими переходами (ДДП) [1]. Система связанных ДДП предполагается состоящей из сверхпроводящих слоев c промежуточными диэлектрическими слоями длины L.

Фазовая динамика системы N ДДП с учетом емкостной и индуктивной связи между контактами описывается начально-краевой задачей для системы дифференциальных уравнений относительно разности фаз $\phi _{l}(x,t)$ и напряжения $V _{l}(x,t)$ на каждом $l$ -ом контакте ( $l=1,2,...N$ ) . В безразмерном виде система уравнений имеет вид [1]:

$\left\{\begin{matrix} \frac{\partial \phi }{\partial t}& = C\cdot V, 0<x<L,t>0\\ \frac{\partial V }{\partial t}& =L^{_{-1}}\frac{\partial^2\phi }{\partial x^2}-\beta V-sin(\phi )+I(t); \end{matrix}\right.$

$\phi =\begin{pmatrix} \phi_{1}\\ \phi_{2}\\ \cdot \cdot \cdot \\ \phi_{N}\\ \end{pmatrix}, V =\begin{pmatrix} V_{1}\\ V_{2}\\ \cdot \cdot \cdot \\ V_{N}\\ \end{pmatrix},$

где L — матрица индуктивной связи, С — матрица емкостной связи:

$L=\begin{pmatrix} 1& S& 0& \cdots& \square& 0& S \\ \vdots& \vdots& \vdots& \vdots& \vdots& \vdots& \vdots&\\ \cdots& 0& S& 1& S& 0& \cdots&\\ \vdots& \vdots& \vdots& \vdots& \vdots& \vdots& \vdots&\\ \square& \square& \square& \square& \square& \square& \square& \\ S& 0& \cdots& \cdots& 0& S& 1& \end{pmatrix}, C=\begin{pmatrix} D^{C}& S^{C}& 0& \cdots& \cdots& 0& 0& S^{C}&\\ \vdots& \vdots& \vdots& \vdots& \vdots& \vdots& \square& \vdots&\\ \cdots& 0& S^{C}& D^{C}& S^{C}& 0& \cdots& \cdots&\\ \vdots& \vdots& \vdots& \vdots& \vdots& \vdots& \vdots& \vdots&\\ \cdots& \cdots& \cdots& \cdots& 0& S^{C}& D^{C}& S^{C}&\\ S^{C}& 0& \cdots& 0& S^{C}& 0& S^{C}& D^{C}& \end{pmatrix},$

β — параметр диссипации, параметр индуктивной связи S принимает значение на интервале 0<|S |<0.5; D ^c— эффективная электрическая толщина ДП, нормированная на толщину диэлектрического слоя; s_c — параметр емкостной связи, $l(t)$ — внешний ток.

Система уравнений дополняется нулевыми начальными условиями и граничными условиями:

$V_{l}(0,t)=V_{l}(L,t)=\frac{\partial \phi (0,t)}{\partial x}=\frac{\partial \phi (L,t)}{\partial x}=0, l=1,2,...,N.$

Также рассматривалась задача, когда граничные условия в направлении x задаются внешним магнитным полем [2].

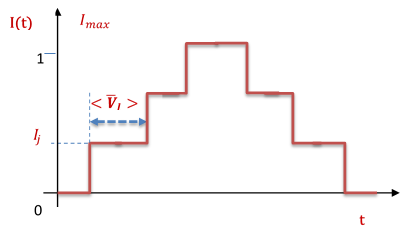
При вычислении вольт-амперных характеристик (ВАХ) зависимость тока от времени выбиралась в виде ступенек (схематичное представление дано на рисунке ниже), т.е. решается задача при постоянном токе ( $I=I_{j}$ ), а найденные функции $\phi_{l},V_{l}(l=1,2,...N)$ берутся в качестве начальных условий для решения зaдачи для тока $&I_{j+1}&$ .

Вычислительная схема и схема распараллеливания. Для численного решения начально-краевой задачи строилась равномерная сетка по пространственной переменной (количество узлов сетки NX ). В системе уравнений (1) производная второго порядка по координате x аппроксимируется с помощью трехточечных конечно разностных формул на дискретной сетке с равномерным шагом $\Delta x$ . Полученная система дифференциальных уравнений относительно значений $\phi_{l},V_{l}(l=1,2,...N)$ в узлах дискретной сетки по x решается методом Рунге–Кутта четвертого порядка.

Для вычисления ВАХ проводится усреднение $V_{l}(x,t)$ по координате и по времени. Для этого на каждом шаге по времени проводится интегрирование напряжения по координате методом Симпсона и усреднение

$\bar{V_{l}}=\frac{1}{L}\int_{0}^{L}V_{l}(x,t)dx,$

далее напряжение усредняется по времени с использованием формулы

$<\bar{V_{l}}>=\frac{1}{T_{max}-T_{min}}\int_{T_{min}}^{T_{max}}\bar{V_{l}}(t)dt$

и затем суммируется по всем ДП. Для интегрирования по времени используется метод прямоугольников.

Схема распараллеливания. При численном решении начально-краевой задачи методом Рунге-Кутта 4-го порядка по временной переменной, на каждом временном слое коэффициенты Рунге-Кутта ( $K_{i}$ ) могут быть найдены независимо (параллельно) для всех NX узлов пространственной сетки и для всех N джозефсоноских переходов. При этом, коэффициенты $K_{i}(i=1,2,3,4)$ определяются один за одним (последовательно). Таким образом, эффективно параллелизация проводится по $NX \cdot N$ точкам. Также при проведении усреднений при расчетах ВАХ, вычисление интегралов может быть проведено в параллельном режиме.

Параллельные реализации. Для ускорения расчетов ВАХ были разработаны параллельные реализации описанной выше вычислительной схемы. Ниже приведены результаты исследования эффективности параллельных реализаций, проведенные при значениях параметров: $L=10;I_{min}=0;I_(max)=1.1;\beta=0.2;N=1;$ $T_(max)=200; \Delta t=0.04$ , количество узлов по пространственной переменной:

NX = 20048.

OpenMP-реализация.
Расчеты проводились:

на вычислительных узлах с процессорами Intel Xeon Phi 7290 (KNL: 16GB, 1.50 GHz, 72 core, поддерживается 4 потока на ядро — всего 288 логических ядер), компилятор Intel (Intel Cluster Studio 18.0.1 20171018);
на двухпроцессорных на вычислительных узлах с процессорами Intel Xeon Gold 6154 (Skylake: 24.75M Cache, 3.00 GHz, 18 core, поддерживается 2 потока на ядро — всего 72 логических ядра на узел).

Ниже приведены графики зависимости ускорения вычислений, получаемое при использовании параллельного алгоритма:

$S=\frac{T_{1}}{T_{n}};$

$T_{1}$ время вычислений с задействованием одного ядра, $T_{n}$ — время вычислений на $n$ -логических ядрах, от количества потоков (число которых равно количеству логических ядер) и график зависимости эффективности использования параллельным алгоритмом вычислительных ядер:

$E=\frac{T_{1}}({n\cdot T_{n})}\cdot100 \% .$

характеризующей масштабируемость параллельного алгоритма.

На Рис.1 и Рис. 2 представлены зависимости ускорения и эффективности от количества потоков при проведении вычислений на узлах с процессорами Intel Xeon Phi, а на Рис.3 и Рис.4 ускорение и эффективность при подключении возможности использования инструкции AVX-512. Отметим, что использование этой инструкции позволило сократить время расчетов в среднем в 1.8 раза.

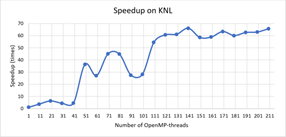
Рисунок 1 — Рис. 1. График зависимости **ускорения** параллельных вычислений от количества потоков

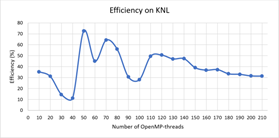
Рисунок 2 — Рис. 2. График зависимости **эффективности** использование параллельным алгоритмом вычислительных ядер от количества потоков

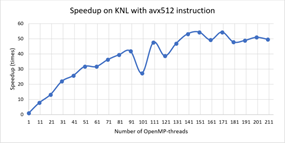
Рисунок 3 — Рис. 3. График зависимости **ускорения** параллельных вычислений от количества потоков. Компиляция программы с опцией — xMIC-AVX512

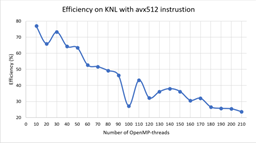
Рисунок 4 — Рис. 4. График зависимости **эффективности** использование параллельным алгоритмом вычислительных ядер от количества потоков. Компиляция программы с опцией — xMIC-AVX512

На Рис.5 и Рис. 6 представлены зависимости ускорения и эффективности от количества потоков при проведении вычислений на узлах с процессорами Intel Xeon Gold 6154.

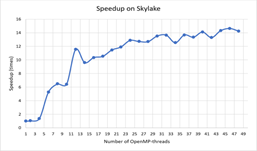
Рисунок 5 — Рис. 5. График зависимости **ускорения** параллельных вычислений от количества потоков

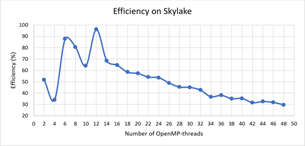
Рисунок 6 — Рис. 6. График зависимости **эффективности** использование параллельным алгоритмом вычислительных ядер от количества потоков

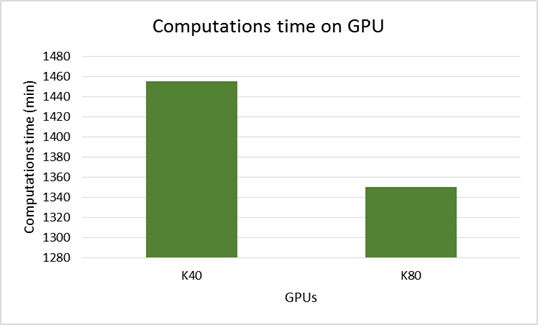
CUDA-реализация. Для расчетов на графических ускорителях от NVIDIA была разработана CUDA-реализация параллельного алгоритма. При вычислениях интегралов использовался алгоритм параллельной редукции с использованием shared memory. Времена расчетов на графических ускорителях NvidiaTesla K40 и NvidiaTesla K80 представлены на диаграмме ниже.

Сравнительный анализ параллельных реализаций. В таблице 1 приведены результаты минимальных времен расчетов, полученных на различных вычислительных архитектурах.

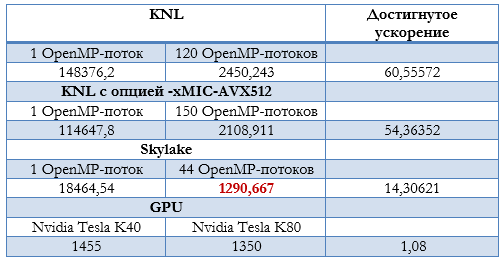
Таблица 1. Наилучшие (минимальные) времена расчетов, полученные на различных вычислительных архитектурах (в минутах) и соответствующие ускорения вычислений.

Таблица 2. Времена расчетов (в минутах) на одном OpenMP потоке процессора Intel Xeon Gold 6154(Skylake) и графических ускорителях Nvidia Tesla K40 и Nvidia Tesla K80.

Наилучшее (минимальное) время для представленных выше значений параметров расчета ВАХ ДДП составляет 1290 минут и было достигнуто при вычислениях на двухпроцессорном узле с процессорами Intel Xeon Gold 6154.

[1] И. Р. Рахмонов, Ю. М. Шукринов, П. Х. Атанасова, Е. В. Земляная, М. В. Башашин, Влияние индуктивной и емкостной связи на вольтамперную характеристику и электромагнитное излучение системы длинных джозефсоновских переходов, Журнал Экспериментальной и Теоретической Физики, Том 151, № 1, 151-159, (2017)

[2] Gh. Adam, M. Bashashin, D. Belyakov, M. Kirakosyan, M. Matveev, D. Podgainy, T. Sapozhnikova, O. Streltsova, Sh. Torosyan, M. Vala, L. Valova, A. Vorontsov, T. Zaikina, E. Zemlyanaya, M. Zuev. IT-ecosystem of the HybriLIT heterogeneous platform for high-performance computing and training of IT-specialists. CEUR Workshop Proceedings (CEUR-WS.org) (2018 г.)

[3] М. В. Башашин, Е. В. Земляная, И.Р. Рахмонов, Ю.М. Шукринов, П. Х. Атанасова, А. В. Волохова, Вычислительная схема и параллельная реализация для моделирования системы длинных джозефсоновских переходов, Компьютерные исследования и моделирование (Computer Research and Modeling), Том 8, № 4, 593–604, (2016)

[4] E. V. Zemlyanaya, M. V. Bashashin, I. R. Rahmonov, Yu. M. Shukrinov, P. Kh. Atanasova, and A. V. Volokhova, Model of stacked long Josephson junctions: Parallel algorithm and numerical results in case of weak coupling, AIP Conference Proceedings, vol 1773, 110018, (2016)